1 引 言
MEMS器件是通过单晶硅等材料由化学汽相沉积、溅射、电镀等方法形成薄膜后经过光刻、蚀刻、牺牲层腐蚀、体硅腐蚀等方法释放形成各种微机械结构而制作的。通过表面微机械加工制备的薄膜往往存在不可忽视的残余内应力和应力梯度,它对器件的成品率和性能的影响很大[123]。由于残余应力和梯度的大小受到加工工艺条件等制约,所以如何实现对结构残余应力和应力梯度的精确在线测量成为MEMS测试的重要任务。目前应用最多的测量薄膜残余应力的方法是基底弯曲法,即在基底上淀积薄膜后通过测量基底的曲率,然后应用Stoney方程计算出薄膜的残余应力[425]。在对薄膜的应力特性进行测量时,都需要通过拟合得到结构的曲率值[227]。本文着重介绍一种基于显微干涉和有限差分技术,以单层微悬臂梁作为测试器件的曲率测试方法。
微悬臂梁在残余应力和应力梯度的作用下会发生弯曲,通过测量弯曲量,即可进一步求得曲率。微悬臂梁结构是MEMS中最基本的可动结构,由此成为很多MEMS器件的关键结构,如谐振器、RF开关以及某些生化传感器等等[8]。又因为其结构简单,建模方法成熟,所以多选择悬臂梁作为测试结构。而显微干涉法利用光波干涉的方法来测量表面形貌,是一种具有较高测量精度和较好空间分辨率的非接触测量方法,并且测量简单快捷,可以用于精确测量悬臂梁表面的弯曲变形量[9210]。使用有限差分法对悬臂梁的二维模型进行分析,可得到梁弯曲量与曲率之间的关系。将测量得到的弯曲信息与模拟的弯曲量进行对比,使用一定的数值最优化方法或者最小二乘法可求得悬臂梁曲率的最佳匹配值。在表面微加工而成的微悬臂梁组上进行的测试实验结果证实了此方法的可行性和准确性。
2 方 法
基于显微干涉法的微悬臂梁曲率测试方法分为三个步骤:首先使用显微干涉法测量悬臂梁上各点的垂直高度信息,即梁的弯曲量,然后分析出弯曲量与曲率的解析关系,最后使用一定的数值计算方法求得曲率值。
2.1 弯曲量测量
使用相移显微干涉法可以准确而方便地测量出微悬臂梁的表面弯曲信息(参考图1的相移显微干涉原理),通过驱动电路驱动参考镜产生次波长量级的光程变化,可获得一组包含被测表面高度信息的干涉条纹图像,然后由干涉图的光强信息解算出被测表面的相位值,提取出包裹的相位信息,最后通过一定的相位解包裹算法得到被测表面真实的相位信息和对应的表面高度[9]。

然而,此时得到的梁面高度信息还不是所需的弯曲量,因为未经过调平处理而直接得到的表面轮廓信息往往存在一定的倾斜误差,这给后续的计算带来较大误差。所以,接下来可使用最小二乘法确定调平基准面,结合坐标旋转重构表面信息的方法消除倾斜误差[11]。如此便得到了整个梁相对于基底平面的弯曲数据。
2.2 有限差分法解析
微悬臂梁(如图2所示)的变形符合小变形原理,满足Bernoulli2Euler方程[627]:

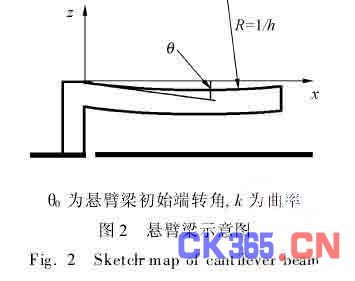
由于悬臂梁在z向的变形相对于梁的长度实际上是非常小的,所以可将梁上各点的曲率k视为相对于x的常数。如图3所示,将悬臂梁分成N个单元,在梁的各个结点上应用有限差分法即可求得梁的弯曲量(挠度)z(x)与曲率k(x)及梁初始端转角θ0之间的解析关系[12]。

图3中结点-1是个虚结点,λ是各结点之间的间距。根据一阶及二阶导数的差分公式:


然后引入边界条件:梁初始端的位移为零,然而初始端的转角往往不为零,即:

使用Mathematica软件将边界条件代入差分方程组可解算出梁上各点挠度的规律解:

如此得到了梁的弯曲量与梁初始端转角θ0以及曲率k之间的关系式,将由这两个量表示的弯曲数据与干涉测量得到的弯曲量比较,使用一定的数值计算方法即可得到梁初始端转角θ0以及曲率k的解。
2.3 数值方法求解
提取悬臂梁的曲率k及初始端转角θ0精确值的思想是:将用显微干涉法获得的梁面弯曲量与上部分中解析出来的弯曲量表达式进行比较,当两者之间的差值最小时所取的k和θ0值即为要求的最佳值。也就是说,将梁的中轴线的弯曲量与公式模拟的弯曲量逐点对比,取使得均方根差值最小的k和θ0值为最终解。均方根差值的表达式见式(15),其中f为弯曲量的测量值与解析模拟值之间的均方根差值,z(xi)是悬臂梁xi处的弯曲测量值。

使用两种方法来实现这一求解:拟牛顿算法和最小二乘法。拟牛顿算法是一种数值最优化的方法,可用于求解如式(15)所示函数的最小值问题。根据这种方法可以得到f的下降方向,即使得f的值变小的方向。只要从某个初值出发,按照使目标函数f的值下降的原则进行查找,即可得到这个无约束问题的极限解或稳定解。
如果将式(15)构造成一个超定方程组,如式(16)所示,也可以使用最小二乘法得出其近似解。

3 实验及结果分析
本实验室自行搭建的一套光学干涉测量系统如图4所示,其中(a)为系统的原理框图,(b)为实物照片。此系统由计算机、显微镜系统、频闪成像同步控制系统、图像采集与数据采集系统、驱动控制系统等结合相应的软件控制和分析模块构成,运用频闪和相移等干涉测量方法可以实现MEMS静态和动态测试[9,13]。应用Mirau干涉显微物镜的相移测试功能,可以方便快捷地测得微悬臂梁表面精确的高度信息。

图5为一组微悬臂梁的干涉图(右侧为基底部分),所用物镜的放大倍数为20,使用本方法对其中的1号和2号悬臂梁进行了测量。首先,对初始得到的表面轮廓以基底平面作为基准调平并使用中值滤波去除噪声之后的表面弯曲轮廓如图6和图7所示。

然后,使用Matlab软件对两个悬臂梁中轴线的弯曲数据进行分析。通过fminunc函数运用拟牛顿算法处理时,设定查找终止时容许的均方根差值为1.5 mm/pixel,可得1号悬臂梁的初始端转角θ0=-53.838μrad,k=-2.366 0
然后,使用Matlab软件对两个悬臂梁中轴线的弯曲数据进行分析。通过fminunc函数运用拟牛顿算法处理时,设定查找终止时容许的均方根差值为1.5 mm/pixel,可得1号悬臂梁的初始端转角θ0=-53.838μrad,k=-2.366 0 ;2号悬臂梁θ0= - 16. 477μrad,k=-2.758 2
;2号悬臂梁θ0= - 16. 477μrad,k=-2.758 2
。使用直接左除的方法求最小二乘近似解,可得1号悬臂梁θ0=-50.473μrad,k=-2.389 7
。使用直接左除的方法求最小二乘近似解,可得1号悬臂梁θ0=-50.473μrad,k=-2.389 7
; 2号悬臂梁θ0= - 18. 168μrad,k=-2.789 0
; 2号悬臂梁θ0= - 18. 168μrad,k=-2.789 0
。两种方法所得的结果基本一致,由此可知1号和2号微悬臂梁的曲率半径分别约为0.42 m和0.36 m,此结果对于同样工艺条件加工出来的两个悬臂梁来说是比较真实可信的。
。两种方法所得的结果基本一致,由此可知1号和2号微悬臂梁的曲率半径分别约为0.42 m和0.36 m,此结果对于同样工艺条件加工出来的两个悬臂梁来说是比较真实可信的。

虽然实验中用到的悬臂梁与其支撑部分的连接处是平整的,但很多表面微加工工艺制备出来的悬臂梁与支撑的连接处存在一个台阶,于是梁的初始端真正的第一个像素可能并不可知,这样可能给测量带来一定的误差。实验中比较了在1号悬臂梁的根部偏移一定数量的像素后得到的初始端转角及曲率值,结果见表1(整个梁长的像素为1 100个)。
从结果可以看出,在x方向偏移一定的像素数得到的初始端转角变化较大,但对于曲率的影响并不明显(偏移的像素数不多的情况下)。所以,在对初始端转角的测量精度要求不高时,不以梁与支撑的连接点作为真正的起始点进行数据分析带来的误差并不大。
4 结论
本文提出的基于显微干涉法测量微悬臂梁曲率的方法,使用自行搭建的光学显微干涉系统实现对梁表面弯曲数据的精确测量,运用两种数值计算方法进行数据处理和比较,得到了测量弯曲量和理论模拟弯曲量之间的均方根差值在每像素1.5 nm以内的曲率值,所得结果准确可信。此方法同样适用于微米宽度、纳米厚度的悬臂梁的曲率测量,并为后续使用单层梁进行薄膜残余应力、应力梯度和杨氏模量等机械力学特性测试的工作打下了基础。
参考文献:
[1] 张泰华,杨业敏,赵亚溥,等.MEMS材料力学性能的测试技术[J].力学进展,2002, 32(4): 5452562.
ZHANG T H, YANG Y M, ZHAO Y P,et al.. Measurement of mechanical properties of MEMS materials[J].Advances in Mechanics,2002,32(4):5452562.(in Chinese)
[2] 向鹏,金春水.Mo/ Si多层膜残余应力的研究[J].光学精密工程, 2003, 11(1): 62267.
XIANG P, JIN CH SH. Measurement of residual stress in molybdenum/silicon multilayer coatings[J].Opt. Pre2cision Eng., 2003, 11(1): 62267. (in Chinese)
[3] 钱劲,张大成,赵亚溥,等.微电子机械系统中的残余应力问题[J].机械强度,2001,23(4):3932401.
QIAN J, ZHANG D CH, ZHAO Y P,et al.. Residual stresses in micro2electro2mechanical systems[J].Journalof Mechanical Strength,2001,23(4):3932401. (in Chinese)
[4] CHEN K S, OU K S. Modification of curvature2based thin2film residual stress measurement for MEMS applications[J].Journal of Micromechanics and Microengineering,2002,12:9172924.
[5] 王莎莎,陈兢,栗大超,等.基于局部基底弯曲法的高灵敏度薄膜应力测试技术[J].半导体学报,2006,27(6):112921135.
WANG SH SH, CHEN J, LI D CH,et al.. A highly sensitive local curvature metrology for internal stress detec2tion in thin films[J].Chinese Journal of Semiconductors,2006,27(6):112921135.(in Chinese)
[6] JENSEN B D, DEBOER M P, MASTERS N D,et al.. Interferometry of actuated microcantilevers to determinematerial properties and test structure nonidealities in MEMS[J].Journal of MicroElectroMechanical Systems,2001,10(3):3362346.
[7] BAKER M S, DEBOER M P, SMITH N F,etal.. Integrated measurement2modeling approaches for evaluating re2sidual stress using micromachined fixed2fixed beams[J].Journal of MicroElectroMechanical Systems,2002,11(6):7432753.
[8] 温志渝,费龙,钟先信,等.集成硅微悬臂梁融合式传感器制造技术[J].光学精密工程,1995, 3(2): 47250.
WEN ZH Y, FEI L, ZHONG X X,et al.. Productive technique for integrated micro2machining silicon cantileverhybrid sensor[J].Opt.Precision Eng., 1995, 3(2): 47250. (in Chinese)
[9] 胡春光.利用相移显微干涉术和频闪成像技术研究MEMS离面运动[D].天津大学硕士论文,2004.
HU CH G.Study on out2of plane motion in MEMS using phase2stepping microscopic interferometry and strobo2scopic imaging technique[D]. Tianjin University Graduate School, 2004. (in Chinese)
[10] 周明宝.干涉法表面形貌测量使用的扩展深度测量范围的方法[J].光学精密工程, 1999, 7(4): 128.
ZHOU M B. Method for expanding the depth measuring range in the surface topography measurement by interfer2ometry[J].Opt.Precision Eng., 1999, 7(4): 128. (in Chinese)
[11] 黄玉波,栗大超,胡小唐,等.微/纳结构表面32D轮廓测量中倾斜误差的补偿方法[J].天津大学学报,2006, 39(10): 123721240.
HUANG Y B, LI D CH, HU X T,et al.. Compensation for tilt errors in MEMS/NEMS 3D profile measurement[J].Journal of Tianjin University,2006,39(10):123721240.(in Chinese)
[12] 薛强.弹性力学[M].北京:北京大学出版社,2006.
XUE Q。Elastic Mechanics[M]. Beijing: Beijing University Press, 2006. (in Chinese)
[13] GUO T, HU CH G, HU X D,et al.. Stroboscopic phase2shifting interferometry for dynamic MEMS character2ization[C].Proceedings of the Fourth International Workshop on Microfactories, Shanghai, P。R。 China:IWMF,2004:6222627.
作者简介:黄玉波(1981-),女,湖南人,天津大学博士研究生,专业方向为测试计量技术及仪器. E2mail:bobohyb@ya2hoo、com、cn、
胡小唐(1952-),男,山西人,天津大学教授,博士生导师,研究方向为微纳测试与加工技术、精密测控技术.E2mail:xthu@tju、edu、cn
通讯作者:栗大超(1976-),男,河南人,天津大学博士,副教授,研究方向为微米纳米技术. E2mail:dachao.li@case、edu、








