本文重点介绍变压器压降及相关常见问题。 变压器电压降是影响变压器效率和性能的重要因素。
导致变压器电压下降的原因很多。 两个最重要的因素是负载和电源的内部电阻。 单相变压器与三相变压器的电压降测量值略有不同。 两个变压器电压降都是电流、电抗和电阻的函数。
什么是变压器压降?
变压器初级绕组和次级绕组中的负载电阻和累积串联电阻导致变压器电压下降。 这些是由不适当的互感引起的。
变压器电压降也称为“电压调节”,因为负载电阻增加导致的电压下降。 电压调节显示发生在变压器次级绕组/负载中的电压降量。 变压器压降也受 I2R 损失。
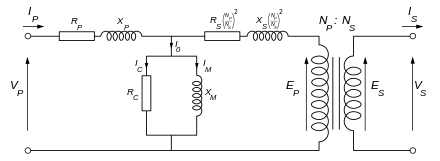
真实变压器的等效电路
变压器电压下降的原因?
电源的内部电阻是电路中电压降的主要原因。 我们从电源中汲取的电流越多,内部电阻上的电压降越多,总电源电压就越小。
如果有一个小负载连接在变压器的次级绕组上,负载阻抗会感应电流流过内部绕组。 由于变压器内部线圈的阻抗,电压下降。 此外,漏抗也是输出端电压变化的原因。
阅读更多…互感变压器:互感等效电路和 10 多个关键常见问题解答
变压器公式中的电压降?
变压器电压降是影响电气系统效率的重要因素。 变压器中过大的电压降可能导致系统中存在负载的部分电压过低。
变压器压降计算公式——
单相变压器:电压降 V_{d}= I\left ( R\cos \theta + X\sin \theta \right )
三相变压器:电压降 V_{d}= \sqrt{3} I\left ( R\cos \theta + X\sin \theta \right )
其中:
Vd = 电压降
R =电阻
X = 电抗
Θ = 功率因数角
如何计算变压器的电压降?
我们可以用近似或精确的形式计算变压器中的电压降。 我们需要知道电阻和电抗来找出任何类型的变压器电压降。
变压器初级侧的近似电压降 = I_{1} R_{01} \cos \theta \pm I_{1} X_{01} \sin \theta 和二次侧 = I_{2} R_{02} \cos \theta \pm I_{2} X_{02} \sin \theta
准确的变压器电压降 =\left ( I_{2} R_{02} \cos \theta \pm I_{2} X_{02} \sin \theta \right ) + \frac{ \left ( I_{2} X_{02} \cos \theta \mp I_{2} R_{02} \sin \theta \right )^{2} } {2\: _{0}^{}\textrm{} V_{2}}
变压器中的近似电压降?
空载时,原边感应电压与外加电压相同,副边感应电压与副边端电压相同。 假设,在空载时, 0V2 是次级端电压。 所以,我们可以说 E2 = 0V2. 让我们说V2 是有载次级电压。 图 1 描绘了称为次级的变压器的相量图。
在图 1 中,R02 和X.02 分别是变压器的净等效电阻和电抗,以次级侧为参考。 将中心保持在 O 处,我们画一条与延伸的 OA 在 H 处相交的弧。从 C 开始,我们在 OH 上画一条垂直线,与它在 G 处相交。现在 AC 代表确切的下降,AG 代表近似下降。
变压器的近似电压降
= AG = AF+ FG = AF+ BE
= \left ( I_{2} R_{02} \cos \theta + I_{2} X_{02} \sin \theta \right )
这是滞后功率因数的近似电压降。
对于超前功率因数,近似电压降为 \left ( I_{2} R_{02} \cos \theta - I_{2} X_{02} \sin \theta \right )
(“+”号代表滞后功率因数,“-”号代表超前功率因数)
同样,我们可以找到称为初级的电压降为 \left ( I_{1} R_{01} \cos \theta \pm I_{1} X_{01} \sin \theta \right )
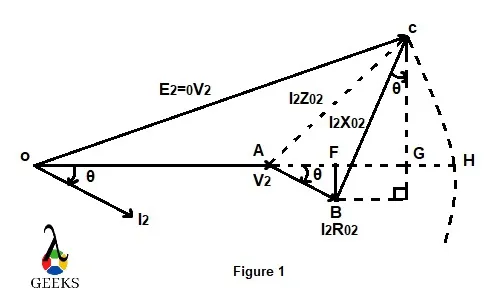
精确和近似的变压器压降 - 相量图
变压器的确切电压降?
根据图 1,确切的电压降为 AH。 我们可以通过将GH添加到已经获得的AG来找到AH。
由直角三角形OCG。 我们有
OC2 = OG2 + 气相色谱2
即超频2 – OG2 = GC2
即 (OC – OG)(OC + OG) = GC2
即 (OH –OG)(OC + OG) = GC2
即GH.2.OC=GC2 [考虑。 OC = OG]
即 GH = \frac{GC^{2}} {2OC}= \frac{\left ( CE-GE \right )^{2}} {2OC}= \frac{\left ( CE-BF \right )^{ 2}} {2OC}= \frac{ \left ( I_{2} X_{02} \cos \theta - I_{2} R_{02} \sin \theta \right )^{2} } {2\: _{0}^{}\textrm{} V_{2}}
对于滞后功率因数,确切的电压降为 = AG+ GH = =\left ( I_{2} R_{02} \cos \theta + I_{2} X_{02} \sin \theta \right ) + \frac{ \left ( I_{2} X_{02} \cos \ theta - I_{2} R_{02} \sin \theta \right )^{2} } {2\: _{0}^{}\textrm{} V_{2}}
对于超前功率因数,确切的电压降为
=\left ( I_{2} R_{02} \cos \theta - I_{2} X_{02} \sin \theta \right ) + \frac{ \left ( I_{2} X_{02} \cos \ theta + I_{2} R_{02} \sin \theta \right )^{2} } {2\: _{0}^{}\textrm{} V_{2}}
通常,确切的电压降为 =\left ( I_{2} R_{02} \cos \theta \pm I_{2} X_{02} \sin \theta \right ) + \frac{ \left ( I_{2} X_{02} \cos \theta \mp I_{2} R_{02} \sin \theta \right )^{2} } {2\: _{0}^{}\textrm{} V_{2}}.
















