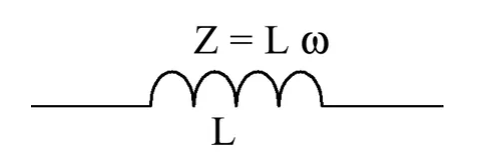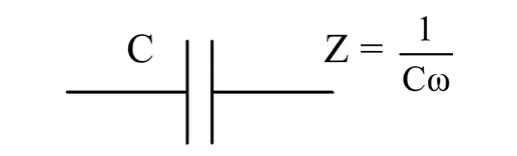阻抗电压是变压器的一个重要参数，也称短路电压，它表示变压器通过额定电流时在变压器自身阻抗上所产生的电压损耗（百分值）。那么什么是电路的阻抗电压？下面一起来了解一下电路的阻抗电压计算方式。

一、什么是电路的阻抗电压？

阻抗是电路或电路元件的有效电阻，其电阻随不同频率的变化而变化 AC. 阻抗也可能是由于欧姆电阻和电抗的综合影响。 阻抗由字母“Z”表示。

由于阻抗是与频率相关的电阻，因此电压电流和阻抗之间的关系可以通过欧姆定律定义为V=IZ。

其中 V 是 电压下降 穿过阻抗，I 是穿过阻抗的电流，Z 是阻抗，虽然 V=IZ 是标量方程，因为我们知道阻抗是频率的函数，那么它也可以定义为 [latex] v(\omega) = i(\omega)z(\omega) [/latex]。

可以为任何可以包含电阻器、电容器或电感器的双端口无源网络定义阻抗。 当网络被压缩成一个组件时，该组件上的电压降就是阻抗电压。

电阻器的阻抗不包含任何虚部，因为阻抗的大小为 R，并且所有频率的相位角为零。 在电容器的阻抗与频率有关的情况下，电容器阻抗随着频率的增加而减小。 而电感是线圈的阻抗，电感的阻抗与频率成正比，也就是说频率越广，阻抗就越高。

二、如何计算阻抗电压 ?

阻抗电压可以借助整个电路的等效阻抗来计算。

如果在一个双端口网络的阻抗 系列 必须计算，然后 串联组合的等效阻抗可以计算为  [latex] Z_{eq} = Z_1 +Z_2+ ….. Z_n, [/latex]  其中每个组件的阻抗相加得到串联连接的等效阻抗。

如果两端口网络的阻抗在 并行 必须计算组合，然后找到 并联组合的等效阻抗为 [latex] \frac{1}{Z_{eq}}= \frac{1}{Z_1} +\frac{1}{Z_2} + …. +\frac {1} {Z_n}. [/latex]

电路的阻抗可以是对于仅包含一个电阻器的电路，Z = R。

[latex] Z = X_C [/latex] 对于仅包含电容器的电路，[latex] X_C [/latex] 是电路的阻抗 电容器.

[latex] Z = X_L [/latex] 对于仅包含电感的电路，[latex] X_L [/latex] 是电感的阻抗。

感抗 [latex] X_L [/latex] 可以定义为 [latex] X_L = i \omega L = 2 \pi f L [/latex]

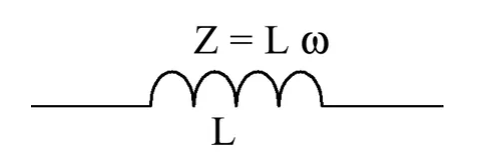
阻抗电感

电容电抗 [latex] X_C [/latex] 可以定义为 [latex] X_C = 1/i \omega C = 1 / I 2 \pi f L [/latex]

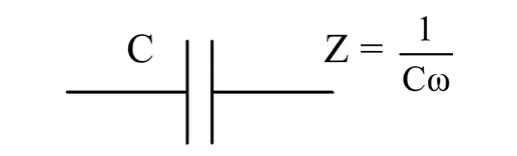
阻抗冷凝器

包含寄存器和电容器串联的电路 [/latex]Z^2 = R^2 +X_C^2 [/latex]

串联电阻和电感的电路 [/latex]Z^2 = R^2 +X_L^2[/latex]

该电路包含 串联电阻电容和电感 然后 [/latex]Z^2 = R^2 + (|X_L – X_C|)^2[/latex]

R中的 交流电路 可以相对于电压定义为 [latex] R = \frac{change in voltage}{ current}.[/latex]

在分析整个电路后，将相似的电抗值相加得到电路的总阻抗，同时计算考虑到电路设计的总阻抗，例如其组件是否相互并联或串联组合。

用于计算电感器和电容器串联的总阻抗，然后减去 感应电抗 和彼此的容抗。

两端电路网络阻抗可以是一个复数，因此可以用相位和幅度特性来表示阻抗。

在借助欧姆定律计算出电路的整体阻抗后，阻抗上的电压降可以通过阻抗已知的电流来计算。

两端电路网络阻抗可以是一个复数，因此可以用相位和幅度特性来表示阻抗。

[/latex]V= IZ = I|Z|e^{j arg (Z)}[/latex]

哪里 |Z| 是阻抗的大小，相量可以通过[latex] \theta = arg (Z)的相位电压来描述电流滞后。[/latex]

三、如何根据电压和电流计算阻抗 ?

双端口网络的阻抗可以用不同的参数表示来计算。

根据 Z 参数或开路阻抗参数，任意两端口网络的输入和输出电压可表示为 [/latex]V_1[/latex] 和 [/latex]V_2[/latex] 可以用输入和输出电流表示 [/latex]I_1[/latex] 和 [/latex]I_2[/latex] 如：

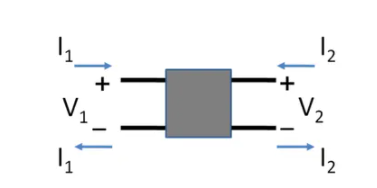
双端口网络的阻抗

[/latex][V] = [Z] [I][/latex]

其中 [Z] 是阻抗矩阵。

[/latex]\开始{bmatrix}

V_1\\

V_2\end{bmatrix} =\begin{bmatrix}

Z_{11} & Z_{12} \\

Z_{21} & Z_{22}

\end{bmatrix}\begin{bmatrix}

\end{bmatrix}[/latex]

用这种方法 整个双端口网络用一个矩形框表示，以及来自网络每个输入或输出端口的电流和电压方向。 

从矩阵中获取方程：

[/latex]V_1 = Z_{11} I_1 + Z_{12} I_2[/latex]

[/latex]V_2 = Z_{21} I_1 + Z_{22} I_2[/latex]

现在假设两端口的输出为开路开路，所以[latex] I_2 = 0 [/latex]

所以现在 [latex] Z_{12} = \frac{V_1}{I_1} [/latex]

[/latex]I_2 = 0，Z_{21} = \frac{V_2}{I_1} [/latex]

现在，假设二端口的输入是开路开路，所以[latex] I_1 = 0 [/latex]

所以现在 [latex] Z_{12} = \frac{V_1}{I_2} [/latex]

而且，现在 [latex] Z_{22} = \frac{V_2}{I_2} [/latex]

[/latex]Z_{11}、Z_{12}、Z_{21}、[/latex] 和 [/latex]Z_{22} [/latex] 也称为二端口网络的阻抗参数或开路参数。

已知[latex] I_1 [/latex]和[latex] I_2的值，可以根据需要计算出V_1 [/latex]或[latex] V_2 [/latex]。