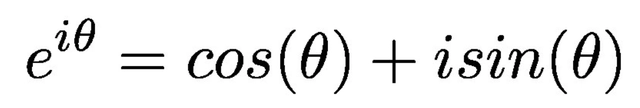什么是欧拉公式？欧拉公式是欧哈德·欧拉在十八世纪创造的，是数学界最着名、最美丽的公式之一。之所以如此，是因为它涉及到各种显然非常不同的元素，比如无理数e、虚数和三角函数。复变函数中，e^(ix)=(cos x+isin x)称为欧拉公式，e是自然对数的底，i是虚数单位。

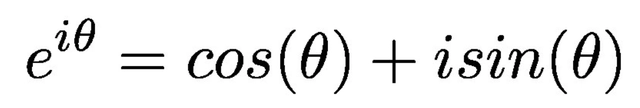
   欧拉定理

   1. 定义

   对任意两个正整数 a, n，如果两者互质，那么 aφ(n)≡1(mod n)。

   2. 证明

   先设集合P为小于n且与n互质的正整数集合{q1 , q2 , q3 , … , qφ(n)},这个集合有两个性质：

   qi与n互质

   qi模n后各不相同

   再设集合Q为{a*q1%n , a*q2%n , a*q3%n , … , a*qφ(n)%n}

   可证：

   因为a与n互质，所以a*q%n也与n互质，即Q中各元素均与n互质

   通过反证法，若a*qi%n=a*qj%n,那么

   a*qi-a*qj=0 --> a*(qi-qj)=0 --> qi-qj=0 --> qi=qj

   因为先前集合P中qi各不相同，所以不成立，可得集合Q中元素各不相同

   由上可得P，Q均为包含φ(n)个小于n且n互质且各不相同的元素集合，而这样的集合只有一个，可得P=Q；

   所以集合P元素的乘积和集合Q元素的乘积相等：

   q1 * q2 * q3 * … * qφ(n)=(a*q1%n) * (a*q2%n) * (a*q3%n) * … * (a*qφ(n)%n)

   q1 * q2 * q3 * … * qφ(n)=aφ(n) * (q1 * q2 * q3 * … * qφ(n))%n

   同时除q1-qφ(n)即可得

   aφ(n)≡1(mod n)

   3.3费马小定理

   若存在整数a,p，a为整数，p为质数，那么a(p-1)≡ 1(mod p)。

   费马小定理是欧拉定理的一种特殊情况（当n为质数时φ(n)为n-1）

    欧拉公式有4条，分别是：

    （1）分式：

    a＾r/（a-b）（a-c）+b＾r/（b-c）（b-a）+c＾r/（c-a）（c-b）

    当r=0，1时式子的值为0

    当r=2时值为1

    当r=3时值为a+b+c

    （2）复数

    由e＾iθ=cosθ+isinθ，得到：

    sinθ=（e＾iθ-e＾-iθ）/2i

    cosθ=（e＾iθ+e＾-iθ）/2

    此函数将两种截然不同的函数---指数函数与三角函数联系起来，被誉为数学中的“天桥”。

    当θ=π时，成为e＾iπ+1=0 它把数学中最重要的e、i、π、1、0联系起来了。

    （3）三角形

    设R为三角形外接圆半径，r为内切圆半径，d为外心到内心的距离，则：

    d＾2=R＾2-2Rr

    （4）多面体

    设v为顶点数，e为棱数，f是面数，则

    v-e+f=2-2p

    p为亏格，2-2p为欧拉示性数，例如

    p=0 的多面体叫第零类多面体

    p=1 的多面体叫第一类多面体